Probabilidad y Etadística Tec.: 2008

viernes, 12 de diciembre de 2008

miércoles, 10 de diciembre de 2008

Unidad V - Regresion Lineal

Ejercicio de Regresion Lineal:

Pagina 1

Pagina 2

Pagina 3

domingo, 30 de noviembre de 2008

martes, 18 de noviembre de 2008

Valor esperado de una variable aleatoria discreta

Si X es una variable aleatoria, y el experimento aleatorio que determina el valor de X se repite muchas veces, entonces se obtiene una secuencia de valores para X. Puede emplearse un resumen de estos valores, tal como el promedio (media), para identificar el valor central de la variable aleatoria.
La funcion de probabilidad de X puede interpretarse como la proporcion de ensayos en los que
X = x. En consecuencia, en realidad no es necesario realizar el experimento muchas veces con la finalidad de determinar el valor medio de X. La media de X puede calcularsecomo el promedio ponderado de los valores posibles de X, asignando al resultado x un factor de ponderacion
fx(x) = P (X = x).

La media o valor esperado de una variable aleatoria discreta X, denotada por μx o E(X), es

μx = E(X) = Sum. xfx(x)

La media de X puede interpretarse como el centro de la masa del rango de los valores de X. Esto es, si se coloca una masa igual a fx(x) en cada punto x de la recta real, entonces E(X) es el punto donde la recta queda en equilibrio. Por consiguiente, el termino funcion de probabilidad puede interpretarse mediante esta analogia con la mecanica.

Distribucion Hipergeometrica

Distribución hipergeométrica

Por claridad, consideremos el siguiente ejemplo: Tenemos una baraja de cartas españolas (N=40 naipes), de las cuales nos vamos a interesar en el palo de oros (D=10 naipes de un mismo tipo). Supongamos que de esa baraja extraemos n=8 cartas de una vez (sin reemplazamiento) y se nos plantea el problema de calcular la probabilidad de que hayan k=2 oros (exactamente) en esa extracción. La respuesta a este problema es

$\begin{eqnarray}\html{eqn24}{{\cal P}_{rob}}[2 \mbox{ oros en un grupo de $8$\sp... ...{{ \left(\begin{array}{c} N\\ n \end{array}\right)\,}} \nonumber \end{eqnarray}$

En lugar de usar como dato D es posible que tengamos la proporción existente, p, entre el número total de oros y el número de cartas de la baraja

$\begin{displaymath}p=\frac{D}{N}=\frac{10}{40}=\frac{1}{4} \Longrightarrow \left... ...dot p \\ \\ N-D = N\cdot q \qquad (q=1-p) \end{array}\right. \end{displaymath}$

de modo que podemos decir que

$\begin{displaymath}{{\cal P}_{rob}}[k \mbox{ oros en un grupo de $n$\space carta... ...ght)\,}}{{ \left(\begin{array}{c} N\\ n \end{array}\right)\,}} \end{displaymath}$

Este ejemplo sirve para representar el tipo de fenómenos que siguen una ley de distribución hipergeométrica. Diremos en general que una v.a. X sigue una distribución hipergeométrica de parámetros, N, n y p, lo que representamos del modo $X{\leadsto}{ {{\bf HGeo} \left( N,n,p \right)} }$ , si su función de probabilidad es

$\begin{displaymath}{ \mbox{\fbox{$\displaystyle {{\cal P}}[X=k] = \frac{{ \left... ...box{ \ \ si \ }\max\{0,n-Nq\} \leq k \leq \min\{n,NP\} $ } } } \end{displaymath}$

Observación

Cuando el tamaño de la población (N) es muy grande, la ley hipergeométrica tiende a aproximarse a la binomial:

$\begin{displaymath}{ {{\bf HGeo} \left( N,n,p \right)} } \stackrel{N\rightarrow \infty}{\longrightarrow} { {{\bf B} \left( n,p \right)} } \end{displaymath}$

El valor esperado de la hipergeométrica es el mismo que el de la binomial,

$\begin{displaymath}{ {{\bf E} \left[ X \right]} } = np \end{displaymath}$

sin embargo su varianza

$\begin{displaymath}{ {{\bf Var } \left[ X \right]} }= npq\cdot \frac{N-n}{N-1} \end{displaymath}$

no es exactamente la de la binomial, pues está corregida por un factor, $\frac{N-n}{N-1}$ , que tiende a 1 cuando $N\rightarrow\infty$ . A este factor se le denomina factor de corrección para población finita.

Distribucion Binomial

Despues de analizar los ensayos de Bernoulli, podemos definir los siguiente>

Un experimento aleatorio que consiste de n ensayos repetidos tales que

(1) Los ensayos son independientes
(2) Cada ensayo tiene solo dos resultados posibles, denominados "exito" y "fracaso", y
(3) La probabilidad de exito en cada ensayo, denotada por p, permanece constante

recibe el nombre de experimento binomial.

La variable aleatoria X que es igual al numero de ensayos donde el resultado es un exito, tiene una distribucion binomial con parametros p y n = 1, 2, ....
La funcion de probabilidad de X es

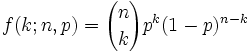
http://www.disfrutalasmatematicas.com/datos/images/binomial-distribution-formula.png

(en terminos de k)

Por otras parte, como cada ensayo del experimento se clasifica en dos resultados, {exito, fracaso}
la distribucion se conoce como "bi - nomial".

Ejemplo:

Ensayos de Bernoulli

Ensayo de Bernoulli

1) Los ensayos son independientes

2) Cada ensayo tiene solo dos resultados posibles denominados ¨exito¨ o ¨fracaso¨.

3) La probabilidad de exito de cada ensayo, denotada por P, permanece constante.

Ejemplo:

La probabilidad de recibir de manera erronea un bit transmitido por un canal digital es 0.1 ademas supongase que los ensayos de transmision son independientes.

Sea la variable aleatoria X = al numero de bits recibidos con error en los proximos cuatro que seran transmitidos, describe el espacio muestral de este experimento e indica el valor de x para cada resultado.

P {Recibir de manera erronea un bit} = 0.1

X = {Numero de bits con error en los proximos 4 que sean transmitidos}

P( X = x)

Combinaciones con != Factorial

P(e) = 0.1
P(c) = 0.9 n = 4

P(X=0) = 1 (0.656)
P(X=1) = 4 (0.0729) = 0.2916
P(X=2) = 6 (0.0081) = 0.0486
P(X=3) = 4 (0.0009) = 0.0036
P(X=4) = 1 (0.0001)

Formula: (n/x) = n!/x!(n-x)! o en terminos de m :

Distribuciones de probabilidad discretas

Distribuciones y Funciones de Probabilidad

A menudo el interes recae en la probabilidad de que una variable aleatoria tome un valor particular.

En el ejemplo de la tabla anterior, el interes puede centrarse en la probabilidad de que ambas caracteristicas sean aprobadas, esto es, en la probabilidad de que X = 2. El conjunto de todos los resultados para los que {X=2} es un evento formado por un solo resultado (aprobado, aprobado). Por consiguiente, la probabilidad del evento {X=2} es 0.64. Esta conclusion puede escribirse como P(X=2) = 0.64.

De manera similar, el conjunto de todos los resultados para los que {X=1} es un evento compuesto por los resultados (aprobado, inaceptable) e (inaceptable, aprobado).

Para el espacio muestral discreto de este ejemplo, la probabilidad de un evento es la suma de las probabilidades de los resultados contenidos en el evento,

P(X=1) = 0.16 + 0.16 = 0.32

Asimismo,

P(X=0) = 0.04

La tabla siguiente presenta un resumen de los valores posibles de la variable aleatoria X del ejemplo anterior, junto con la probabilidad de cada valor (donde los valores {0, 1, 2} son los valores posibles de X). Dado que X debe tomar uno de estos valores, la suma de todas las probabilidades es uno.

Notese que en estos ejemplos la variable aleatoria esta claramente definida. A menudo este es un paso inicial importante en el proceso de determinar una probabilidad.

El evento que esta formado por todos los resultados para los que X = x se denota como {X = x}, y la probabilidad de este evento como P (X = x).

La distribucion de probabilidad o distribucion de una variable aleatoria X es una descripcion del conjunto de valores posibles de X (rango de X), junto con la probabilidad asociada con cada uno de estos valores. A menudo la distribucion de probabilidad de una variable aleatoria es el resumen mas util de un experimento aleatorio. La distribucion de probabilidad de una variable aleatoria pude darse de muchas maneras. Para una variable aleatoria que puede tomar un numero pequeño de valores, lo mas simple es proceder como en el ejemplo anterior, y listar los valores posibles junto con las probabilidades respectivas. En otros casos, es conveniente expresar en terminos de una formula la probabilidad de que la variable aleatoria X tome un valor x.

Ejemplo:

Sea X una variable aleatoria que denota el numero de muestras de aire que es necesario analizar para detectar una molecula rara. Supongase que la probabilidad de que una muestra de aire contenga una molecula rara es 0.01, y que las muestras son independientes. Determine la distribucion de probabilidad de X.

Sean p: unamuestra donde esta presente la molecula rara, y a: una muestra donde la molecula esta ausente. El espacio muestral de este experimento es infinito, y puede ser representado por todas las secuencias posibles que comienzan con una cadena de "a" y terminan con p. Esto es:

S = {p, ap, aap, aaap, aaaap, aaaaap, y asi sucesivamente}

Considerense unos cuantos casos especiales. Se tiene que P (X = 1) = P (p) = 0.01 . Por otro lado, si se emplea la hipotesis de independencia,

P (X = 2) = P (ap) = 0.99 (0.01) = 0.0099

Una formula general es

P (X = x) = P (aa...ap) = 0.99 (elevado a la x - 1), para x = 1, 2, 3, ....

La descripcion de probabilidades asociadas con X en terminos de esta formula es el metodo mas sencillo para describir la ditribucion de X en este ejemplo.

---------------------------------------------------------------------------------------------

Funcion de Probabilidad

En el ejemplo anterior la distribucion de X esta descrita por una formula que expresa la probabilidad como una funcion de x. Esto es, la distribucion de X esta especificada por la funcion fx(x) = P (X = x). El subindice de fx(x) denota la variable aleatoria de interes. El subindice se omitira cuando no exista ninguna confusion sobre la probabilidad del resultado. Dado que fx(x) esta definida como una probabilidad, fx(x) es una funcion que va del conjunto de valores posibles de la variable aleatoria al intervalo [0, 1].

Para una variable aleatoria X, fx(x) satisface las propiedades siguientes:

(1) fx(x) = P (X = x)
(2) fx(x) ≥ 0 para toda x
(3) ∑ fx(x) = 1

Ejemplo de funcion de probabilidad.

Funciones de Distribucion Acumulada

Supongase que en el ejemplo anterior el interes recae en la probabilidad de encontrar una molecula rara en tres muestras o menos. Esta pregunta puede expresarse como P (X ≤ 3).
El evento en que {X ≤ 3} es la union de los eventos {X = 1}, {X = 2}, {X = 3}. Al utilizar la notacion del ejemplo, el evento en que {X = 1} esta formado por un solo resultado p, el evento en que {X = 2} esta formado solo por el resultado ap, y el evento en el que {X = 3} por el resultado aap. Es claro que estos eventos son mutuamente excluyentes.
Por consiguiente,

P (X ≤ 3) = P (X = 1) + P (X = 2) + P (X = 3)

--------- = 0.01 + 0.99 (0.01) + 0.99²(0.01)
--------- = 0.0297

Para este ejemplo, existe una formula general,

P (X ≤ x) = 1 - 0.99ª

El ejemplo anterior ilustra el hecho de que en ocaciones es util expresar probabilidades acumuladas, tales como P(X ≤ x), en terminos de una formula. Por otra parte, el mismo ejemplo muestra que una formula para probabilidades acumuladas puede emplearse para encontrar la funcion de probabilidad de una variable aleatoria. En consecuencia, el uso de probabilidades acumuladas es una alternativa para describir la distribucion de probabilidad de una variable aleatoria. Una funcion que proporciona probabilidades acumuladas tiene un gran valor.
E n general, para cualquier variable aleatoria discreta con valores posibles x1, x2, ...., xn, los eventos {X = x1}, {X = x2},....{X = xn} son mutuamente excluyentes. Por consiguiente,
P(X ≤ x) = ∑ fx(xi).

La funcion de distribucion acumulada de una variable aleatoria discreta X, denotada por Fx(x), es

Fx(x) = P(X ≤ x) = ∑ f(xi)

Para una variable aleatoria discreta X, Fx(x) satisface las propiedades siguientes.

(1) Fx(x) = P(X ≤ x) = ∑ fx(xi)
(2) 0 ≤ Fx(x) ≤ 1
(3) Si x ≤ y, entonces Fx(x) ≤ Fx(y)

Ejemplo de Funcion de Distribucion acumulada

UNIDAD III - Funciones de distribución de probabilidad

Variables aleatorias y su clasificacion

Discreta ---- { X } - Variable aleatoria discreta (se puede contar).

Continua ----{ X } - Variable aleatoria continua (se puede medir) - tiempo, peso, estatura, etc.

Variables aleatorias discretas

Con frecuencia el interes recae en resumir con un numero el resultado de un experimento aleatorio. En muchos de los ejemplos de experimentos aleatorios considerados hasta el momento, el espacio muestral solo es una descripcion de los posibles resultados. En algunos casos las descripciones de los resultados son suficientes, pero en otros es util asociar un numero con cada resultado del espacio muestral. Ya que el resultado de un experimento no se conoce con anticipacion, sucede lo mismo con el valor de la variable. Por esta razon, la variable que asocia un numero con el resultado de un experimento aleatorio se conoce como variable aleatoria.

Una variable aleatoria es una funcion que asigna un numero real a cada resultado en el espacio muestral de un experimento aleatorio.

Las variables aleatorias se denotan con una letra mayuscula, tal como X, y con una letra minuscula, como x, el valor posible de X. El conjunto de los posibles valores de la variable aleatoria X recibe el nombre de rango de X.

Ejemplo:

Se evalua un nuevo proceso para la fabricacion de partes moldeadas en plastico en terminos de la coloracion y reduccion del tamaño. Una de las primeras corridas del proceso proporciona la informacion para el espacio muestral y las probabilidades que aparecen en la tabla.
Supongase que el interes recae en resumir los resultados de este experimento aleatorio con el numero de caracteristicas (de coloracion y reduccion del tamaño) que son aprobadas.
Por lo cual, se define una variable aleatoria, X, para ser igual al numero de caracteristicas aprobadas.

La cuarta columna de la tabla contiene los valores de X asignados a cada resultado del experimento. Por ejemplo, al resultado (aprobado, aprobado) se le asigna x=2.

Ejemplo 2:

El sistema de comunicacion por voz de una empresa tiene 48 lineas externas. En un determinado momento, se observa el sistema y algunas lineas estan ocupadas. Sea X la variable aleatoria que denota el numero de lineas en uso. Entonces X puede tomar cualquier valor entero de cero a 48.

X = {0, 1, 2, 3, 4, 5.....,48}

martes, 14 de octubre de 2008

VIDEOS - UNIDAD II

Espacio Muestral con Diagramas de arbol

Probabilidad mediante Conjuntos

Espacios muestrales con conjuntos

Probabilidad Condicional

Regla de la Probabilidad Total

Ejercicios4

Ejercicio - Probabilidad Condicional

Los resultados obtenidos de 266 muestras de aire se clasifican de acuerdo con la presencia de 2 moléculas

Sea A el evento formado por todas las muestras en las que se encuentra presente la molécula rara 1.

Sea B el evento formado por todas las muestras de aire donde esta presente la molecula rara 2.

Los datos se presentan en la tabla:

Encuentra la probabilidad de A

P (A / B) = 12 / 30

P (B) = n (B) = 30 P (B) = 30 / 266

P (B / A) = 12 / 36 = 1 / 3

Ejercicios - Probabilidad mediante conjuntos

Los eventos compuestos se forman al aplicar las operaciones basicas de los conjuntos a los eventos individuales.
Las uniones, intersecciones y los complementos de eventos son de interes frecuente.
La probabilidad de un evento compuesto a menudo puede obtenerse a partir de las probabilidades de cada uno de los eventos que lo forman. En ocaciones las operaciones basicas de los conjuntos tambien son utiles para determinar la probabilidad de un evento compuesto.

1)
La siguiente tabla presenta la historia de 940 obleas de un proceso de fabricacion de semiconductores. Supongase que se elige al azar una oblea.

Sea A el evento en el que la oblea tiene altos niveles de contaminacion

Sea B el evento en el que la oblea esta en el centro del instrumento

a) ¿Como interpretas A U B Y A ∩ B ?

A U B = {112 + 68 + 246} = 426

A ∩ B = {246}

b) Calcula la probabilidad de cada evento?

P (A) = 112 + 246 / 940 = 358 / 940 = 0.38

P (B) = 68 + 246 / 940 = 314 / 940 = 0.334

P (A U B) = 426 /940 = 0.4531

P (A ∩ B ) = 246 / 940 = 0.2617

Despues de tener entrevistas en dos compañias donde quiere trabajar, el evalua la probabilidad que tiene de obtener un empleo en la compañia A como 0.8 y la probabilidad de tenerla en la compañia B como 0.6 . Si por otro lado, considera que la probabilidad de que reciba ofertas de ambas compañias es de 0.5, ¿ Cual es la probabilidad de que obtenga al menos una oferta de esas dos compañias?

A = compañia 1

B = compañia 2

P (A) = 0.8P (B) = 0.6

P (A ∩ B) = 0.5

P (A U B) = P (A) + P (B) - P (A ∩ B) P (A U B) = 0.9

Ejercicios - Espacio muestral y conjuntos

5)
Una caja tiene 3 pelotas una rosa, una blanca y otra azul.

Se sacan 2 de ellas reemplazándolas, es decir se saca una, se observa su color, se introduce y se saca otra.

Diagrama de árbol:

B = {x} probabilidad de que a primera bola sea blanca.

n (B) = 2

B = {BA, BR}

A = {X / X en rojo y blanco}

n (A) = 2 A = {BR, RB}

Conjuntos:

A U B = {BR, RB, BA} n (A U B) = 3

A ∩ B = {BR} n (A ∩ B) = 1

Las mediciones de tiempo redondeadas al minuto mas próximo necesario para completar una reacción química pueden modelarse utilizando el espacio muestal.

S = {1, 2, 3, 4, .......} conjunto universal Indeterminado

Sean los eventos:

E1 = {X / 1 ≤ X <>

E2 = {X / 3 <>

* Encuentra:

E1 U E2 = {X / 1 ≤ X <>

E1 ∩ E2 = {X / 4 ≤ X <>

E1´ = {X / X ≥ 10}

E1´ ∩ E2 = {X / 10 ≤ X <>

Se analizan muestras de policarbonato y se mide su resistencia a las ralladuras y a los golpes.
Los resultados obtenidos se muestran en la tabla:

Sea el evento A donde la muestra tiene una alta resistencia a los golpes

Sea el evento B donde la muestra tiene una alta resistencia a las ralladuras

Determina:

n (A ∩ B) = 40

n ( A´ ) = 7

n (A ∩ B) = 46

Representa con Diagramas de Venn cada espacio muestral:

Los resultados posibles de un experimento aleatorio son:

S = {a, b, c, d} Con probabilidad 0.1, 0.3, 0.5 y 0.1 respectivamente

P (a) = 0.1 + P (i) = 1
P (b) = 0.3
P (c) = 0.5
P (d) = 0.1

Sea A el evento {a, b} , B el evento {b, c, d} , y C {d}

Encuentra la probabilidad de:

P (A) = 0.1 + 0.3 = 0.4

P (B) = 0.3 + 0.5 + 0.1 = 0.9

P (C) = 0.1

P (A´) = 1 – 0.4 = 0.6

P (B´) = 1– 0.9 = 0.1

P (C´) = 1 – 0.1 = 0.9

P (A ∩ B) = 0.3

P (A U B) = 1

P (A´ ∩ B) = 0.6

P (B´ ∩ A) = 0.1

lunes, 13 de octubre de 2008

Teoria de los conjuntos, Axiomas y teoremas de probabilidad

Como ya lo dijimos, la teoría de conjuntos es de mucha utilidad en el desarrollo de las probabilidades, entonces utilizizando esta teoria, denotamos como $A\cup B$ a la unión de

, que es el conjunto de todos los puntos que pertenecen a

o a

(o a ambos). La intersección $A\cap B$ de estos conjuntos se define como el conjunto de todos los puntos que pertenecen a

y a

simultáneamente. Si $A\cap B = \emptyset{}$ (no contiene puntos),

son mutuamente excluyentes.

Algunas probabilidades que resultan evidentes, en esta notación se expresan como

$\displaystyle P(\emptyset)=0 \;,\qquad P(S)=1 \;.$

$P(A\cap B)$ representará entonces la probabilidad de tener ambos resultados, y $P(A\cup B)$ , la probabilidad de tener como resultado un evento

(o ambos). En particular,

$\displaystyle P(A\cup B) = P(A) + P(B) - P(A\cap B) \;.$

En el caso de que

sean mutuamente excluyentes tendremos $P(A\cup B)=P(A)+P(B)$ .

Si $A_1, A_2, \dots , A_m$ son mutuamente excluyentes y exhaustivos, es decir, cubren todo el espacio muestral y por lo tanto $A_1\cup A_2\cup \cdots\cup A_m = S$ , decimos que $\{A_j\}$ es una partición de en subconjuntos. Cuando $\{A_j\}$ es una partición se cumple que $$P(A_1)+P(A_2)+\cdots+P(A_m)=$ .

son eventos independientes si y sólo si $P(A\cap B)=P(A) P(B)$ .

Se define probabilidad condicional $P(B\vert A)$ como la probabilidad de obtener el resultado dado que también se obtiene :

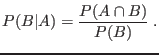
$\displaystyle P(B\vert A) = \frac{P(A\cap B)}{P(B)} \;.$

En esta expresión el denominador de alguna manera sugiere una nueva normalización, como si redujéramos el espacio muestral al evento

. Como $P(A\cap B)=P(B\cap A)$ , puede inferirse la relación

$\displaystyle P(A) P(A\vert B) = P(B) P(B\vert A) \;.$

Evidentemente, en el caso de que

sean independientes, se cumple que $P(B\vert A)=P(A)$ .

Entonces podemos definir con base a la teoria de los conjuntos:

Axiomas de probabilidad:

* P (S) = 1

* 0 ≤ P (E) ≤ 1

* Para dos eventos E1 y E2 con E1 ∩ E2 = Ø

P (E1 ∩ E2 ) = P(E1) + P(E2)

P (0) = Ø

Si E es un evento cualquiera:

P (E´) = 1 - P(E)

Independencia de eventos:
Eventos independientes: dos eventos A y B son independientes sisé la ocurrencia o no ocurrencia afecta la probabilidad asignada a la ocurrencia del otro.

Regla de la adición:

P (A U B) = P (A) + P (B) - P (A ∩ B)

Tres o mas eventos:

P (A U B U C) = P (A) + P (B) + P (C) - P (A ∩ B) - P (A ∩ C) - P (B ∩ C) + P (A ∩ B ∩ C)

Si son mutuamente excluyentes (independientes) :

P (A U B) = Ø

P (A U B) = P (A) + P (B)

Tres o mas eventos:

P (A U B U C) = P (A) + P (B) + P (C)

Probabilidad Condicional:

Muchas veces la probabilidad de que ocurra un suceso viene influida por el hecho de que ocurra o no otro suceso, o por una información adicional.

En general, si A y B son dos eventos , se define la probabilidad condicionada del eveto A sobre el B como la probabilidad de que ocurra A habiendo sucedido antes B:

$\begin{displaymath} \mathbb{P}(A \mid B) = \frac{\mathbb{P}(A \cap B)}{\mathbb{P}(B)} \end{displaymath}$

Regla de la multiplicacion:

Sean A y B dos eventos definidos en el espacio muestral S. Entonces :

P (A ∩ B) = P (B) . P (A/B)

o bien

P (A ∩ B) = P (A) . P (B/A)

Si A y B son eventos independientes entonces:

P (A ∩ B) = P (A) . P (B)

Probabilidad Total:

Sea A1, A2, ...,An un sistema completo de sucesos tales que la probabilidad de cada uno de ellos es distinta de cero, y sea B un suceso cualquier del que se conocen las probabilidades condicionales P(B/Ai), entonces la probabilidad del suceso B viene dada por la expresión:

Ejemplo:

P (F) = P (F ∩ A) + P (F ∩ A´)
= P (F/A) . P (A) + P (F/A´) . P (A´)

Teorema de Bayes:

Sea A1, A2, ...,An un sistema completo de sucesos, tales que la probabilidad de cada uno de ellos es distinta de cero, y sea B un suceso cualquier del que se conocen las probabilidades condicionales P(B/Ai). entonces la probabilidad P(Ai/B) viene dada por la expresión:

$\begin{displaymath} \mathbb{P}(A \mid B) = \frac{\mathbb{P}(B \mid A) \cdot \mathbb{P}(A)}{\mathbb{P}(B)} \end{displaymath}$

P (B) = P (B/A1) . P (A1) + P (B/A2) . P (A2)+...+ P (B/An) . P (An)

o bien:

El teorema de Bayes parte de una situación en la que es posible conocer las probabilidades de que ocurran una serie de sucesos Ai.

A esta se añade un suceso B cuya ocurrencia proporciona cierta información, porque las probabilidades de ocurrencia de B son distintas según el suceso Ai que haya ocurrido.

Conociendo que ha ocurrido el suceso B, la fórmula del teorema de Bayes nos indica como modifica esta información las probabilidades de los sucesos Ai.

En los problemas relacionados con la probabilidad, y en particular con la probabilidad condicionada, así como con la probabilidad total y el teorema de Bayes, es aconsejable que, con la información del problema, construyas una tabla de contingencia o un diagrama de árbol.

Probabilidad y Etadística Tec.