Como ya lo dijimos, la teoría de conjuntos es de mucha utilidad en el desarrollo de las probabilidades, entonces utilizizando esta teoria, denotamos como
Algunas probabilidades que resultan evidentes, en esta notación se expresan como
Si ![]() son mutuamente excluyentes y exhaustivos, es decir, cubren todo el espacio muestral y por lo tanto
son mutuamente excluyentes y exhaustivos, es decir, cubren todo el espacio muestral y por lo tanto ![]() , decimos que
, decimos que ![]() es una partición de
es una partición de ![]() en
en ![]() subconjuntos. Cuando
subconjuntos. Cuando ![]() es una partición se cumple que
es una partición se cumple que ![]() .
.
Se define probabilidad condicional ![]() como la probabilidad de obtener el resultado
como la probabilidad de obtener el resultado ![]() dado que también se obtiene
dado que también se obtiene ![]() :
:
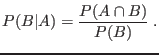
Evidentemente, en el caso de que
Entonces podemos definir con base a la teoria de los conjuntos:
Axiomas de probabilidad:
* P (S) = 1
* 0 ≤ P (E) ≤ 1
* Para dos eventos E1 y E2 con E1 ∩ E2 = Ø
P (E1 ∩ E2 ) = P(E1) + P(E2)
P (0) = Ø
Si E es un evento cualquiera:
P (E´) = 1 - P(E)Independencia de eventos:
Eventos independientes: dos eventos A y B son independientes sisé la ocurrencia o no ocurrencia afecta la probabilidad asignada a la ocurrencia del otro.
Regla de la adición:
P (A U B) = P (A) + P (B) - P (A ∩ B)
Tres o mas eventos:
P (A U B U C) = P (A) + P (B) + P (C) - P (A ∩ B) - P (A ∩ C) - P (B ∩ C) + P (A ∩ B ∩ C)
Si son mutuamente excluyentes (independientes) :
P (A U B) = Ø
P (A U B) = P (A) + P (B)
Tres o mas eventos:
P (A U B U C) = P (A) + P (B) + P (C)
Muchas veces la probabilidad de que ocurra un suceso viene influida por el hecho de que ocurra o no otro suceso, o por una información adicional.
En general, si A y B son dos eventos , se define la probabilidad condicionada del eveto A sobre el B como la probabilidad de que ocurra A habiendo sucedido antes B:
Regla de la multiplicacion:
Sean A y B dos eventos definidos en el espacio muestral S. Entonces :
P (A ∩ B) = P (B) . P (A/B)
o bien
P (A ∩ B) = P (A) . P (B/A)
Si A y B son eventos independientes entonces:
Probabilidad Total:
Sea A1, A2, ...,An un sistema completo de sucesos tales que la probabilidad de cada uno de ellos es distinta de cero, y sea B un suceso cualquier del que se conocen las probabilidades condicionales P(B/Ai), entonces la probabilidad del suceso B viene dada por la expresión:


P (F) = P (F ∩ A) + P (F ∩ A´)
= P (F/A) . P (A) + P (F/A´) . P (A´)
Teorema de Bayes:
Sea A1, A2, ...,An un sistema completo de sucesos, tales que la probabilidad de cada uno de ellos es distinta de cero, y sea B un suceso cualquier del que se conocen las probabilidades condicionales P(B/Ai). entonces la probabilidad P(Ai/B) viene dada por la expresión:
![]()
P (B) = P (B/A1) . P (A1) + P (B/A2) . P (A2)+...+ P (B/An) . P (An)
o bien:

El teorema de Bayes parte de una situación en la que es posible conocer las probabilidades de que ocurran una serie de sucesos Ai.
A esta se añade un suceso B cuya ocurrencia proporciona cierta información, porque las probabilidades de ocurrencia de B son distintas según el suceso Ai que haya ocurrido.
Conociendo que ha ocurrido el suceso B, la fórmula del teorema de Bayes nos indica como modifica esta información las probabilidades de los sucesos Ai.
En los problemas relacionados con la probabilidad, y en particular con la probabilidad condicionada, así como con la probabilidad total y el teorema de Bayes, es aconsejable que, con la información del problema, construyas una tabla de contingencia o un diagrama de árbol.

1 comentario:
mejora tus vídeos esta bien pero no se ve claramente éxito.
Publicar un comentario