Probabilidad y Etadística Tec.: octubre 2008

martes, 14 de octubre de 2008

VIDEOS - UNIDAD II

Espacio Muestral con Diagramas de arbol

Probabilidad mediante Conjuntos

Espacios muestrales con conjuntos

Probabilidad Condicional

Regla de la Probabilidad Total

Ejercicio - Probabilidad Condicional

Los resultados obtenidos de 266 muestras de aire se clasifican de acuerdo con la presencia de 2 moléculas

Sea A el evento formado por todas las muestras en las que se encuentra presente la molécula rara 1.

Sea B el evento formado por todas las muestras de aire donde esta presente la molecula rara 2.

Los datos se presentan en la tabla:

Encuentra la probabilidad de A

P (A / B) = 12 / 30

P (B) = n (B) = 30 P (B) = 30 / 266

P (B / A) = 12 / 36 = 1 / 3

Ejercicios - Probabilidad mediante conjuntos

Los eventos compuestos se forman al aplicar las operaciones basicas de los conjuntos a los eventos individuales.
Las uniones, intersecciones y los complementos de eventos son de interes frecuente.
La probabilidad de un evento compuesto a menudo puede obtenerse a partir de las probabilidades de cada uno de los eventos que lo forman. En ocaciones las operaciones basicas de los conjuntos tambien son utiles para determinar la probabilidad de un evento compuesto.

1)
La siguiente tabla presenta la historia de 940 obleas de un proceso de fabricacion de semiconductores. Supongase que se elige al azar una oblea.

Sea A el evento en el que la oblea tiene altos niveles de contaminacion

Sea B el evento en el que la oblea esta en el centro del instrumento

a) ¿Como interpretas A U B Y A ∩ B ?

A U B = {112 + 68 + 246} = 426

A ∩ B = {246}

b) Calcula la probabilidad de cada evento?

P (A) = 112 + 246 / 940 = 358 / 940 = 0.38

P (B) = 68 + 246 / 940 = 314 / 940 = 0.334

P (A U B) = 426 /940 = 0.4531

P (A ∩ B ) = 246 / 940 = 0.2617

Despues de tener entrevistas en dos compañias donde quiere trabajar, el evalua la probabilidad que tiene de obtener un empleo en la compañia A como 0.8 y la probabilidad de tenerla en la compañia B como 0.6 . Si por otro lado, considera que la probabilidad de que reciba ofertas de ambas compañias es de 0.5, ¿ Cual es la probabilidad de que obtenga al menos una oferta de esas dos compañias?

A = compañia 1

B = compañia 2

P (A) = 0.8P (B) = 0.6

P (A ∩ B) = 0.5

P (A U B) = P (A) + P (B) - P (A ∩ B) P (A U B) = 0.9

Ejercicios - Espacio muestral y conjuntos

5)
Una caja tiene 3 pelotas una rosa, una blanca y otra azul.

Se sacan 2 de ellas reemplazándolas, es decir se saca una, se observa su color, se introduce y se saca otra.

Diagrama de árbol:

B = {x} probabilidad de que a primera bola sea blanca.

n (B) = 2

B = {BA, BR}

A = {X / X en rojo y blanco}

n (A) = 2 A = {BR, RB}

Conjuntos:

A U B = {BR, RB, BA} n (A U B) = 3

A ∩ B = {BR} n (A ∩ B) = 1

Las mediciones de tiempo redondeadas al minuto mas próximo necesario para completar una reacción química pueden modelarse utilizando el espacio muestal.

S = {1, 2, 3, 4, .......} conjunto universal Indeterminado

Sean los eventos:

E1 = {X / 1 ≤ X <>

E2 = {X / 3 <>

* Encuentra:

E1 U E2 = {X / 1 ≤ X <>

E1 ∩ E2 = {X / 4 ≤ X <>

E1´ = {X / X ≥ 10}

E1´ ∩ E2 = {X / 10 ≤ X <>

Se analizan muestras de policarbonato y se mide su resistencia a las ralladuras y a los golpes.
Los resultados obtenidos se muestran en la tabla:

Sea el evento A donde la muestra tiene una alta resistencia a los golpes

Sea el evento B donde la muestra tiene una alta resistencia a las ralladuras

Determina:

n (A ∩ B) = 40

n ( A´ ) = 7

n (A ∩ B) = 46

Representa con Diagramas de Venn cada espacio muestral:

Los resultados posibles de un experimento aleatorio son:

S = {a, b, c, d} Con probabilidad 0.1, 0.3, 0.5 y 0.1 respectivamente

P (a) = 0.1 + P (i) = 1
P (b) = 0.3
P (c) = 0.5
P (d) = 0.1

Sea A el evento {a, b} , B el evento {b, c, d} , y C {d}

Encuentra la probabilidad de:

P (A) = 0.1 + 0.3 = 0.4

P (B) = 0.3 + 0.5 + 0.1 = 0.9

P (C) = 0.1

P (A´) = 1 – 0.4 = 0.6

P (B´) = 1– 0.9 = 0.1

P (C´) = 1 – 0.1 = 0.9

P (A ∩ B) = 0.3

P (A U B) = 1

P (A´ ∩ B) = 0.6

P (B´ ∩ A) = 0.1

lunes, 13 de octubre de 2008

Teoria de los conjuntos, Axiomas y teoremas de probabilidad

Como ya lo dijimos, la teoría de conjuntos es de mucha utilidad en el desarrollo de las probabilidades, entonces utilizizando esta teoria, denotamos como $A\cup B$ a la unión de

, que es el conjunto de todos los puntos que pertenecen a

o a

(o a ambos). La intersección $A\cap B$ de estos conjuntos se define como el conjunto de todos los puntos que pertenecen a

y a

simultáneamente. Si $A\cap B = \emptyset{}$ (no contiene puntos),

son mutuamente excluyentes.

Algunas probabilidades que resultan evidentes, en esta notación se expresan como

$\displaystyle P(\emptyset)=0 \;,\qquad P(S)=1 \;.$

$P(A\cap B)$ representará entonces la probabilidad de tener ambos resultados, y $P(A\cup B)$ , la probabilidad de tener como resultado un evento

(o ambos). En particular,

$\displaystyle P(A\cup B) = P(A) + P(B) - P(A\cap B) \;.$

En el caso de que

sean mutuamente excluyentes tendremos $P(A\cup B)=P(A)+P(B)$ .

Si $A_1, A_2, \dots , A_m$ son mutuamente excluyentes y exhaustivos, es decir, cubren todo el espacio muestral y por lo tanto $A_1\cup A_2\cup \cdots\cup A_m = S$ , decimos que $\{A_j\}$ es una partición de en subconjuntos. Cuando $\{A_j\}$ es una partición se cumple que $$P(A_1)+P(A_2)+\cdots+P(A_m)=$ .

son eventos independientes si y sólo si $P(A\cap B)=P(A) P(B)$ .

Se define probabilidad condicional $P(B\vert A)$ como la probabilidad de obtener el resultado dado que también se obtiene :

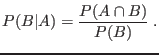
$\displaystyle P(B\vert A) = \frac{P(A\cap B)}{P(B)} \;.$

En esta expresión el denominador de alguna manera sugiere una nueva normalización, como si redujéramos el espacio muestral al evento

. Como $P(A\cap B)=P(B\cap A)$ , puede inferirse la relación

$\displaystyle P(A) P(A\vert B) = P(B) P(B\vert A) \;.$

Evidentemente, en el caso de que

sean independientes, se cumple que $P(B\vert A)=P(A)$ .

Entonces podemos definir con base a la teoria de los conjuntos:

Axiomas de probabilidad:

* P (S) = 1

* 0 ≤ P (E) ≤ 1

* Para dos eventos E1 y E2 con E1 ∩ E2 = Ø

P (E1 ∩ E2 ) = P(E1) + P(E2)

P (0) = Ø

Si E es un evento cualquiera:

P (E´) = 1 - P(E)

Independencia de eventos:
Eventos independientes: dos eventos A y B son independientes sisé la ocurrencia o no ocurrencia afecta la probabilidad asignada a la ocurrencia del otro.

Regla de la adición:

P (A U B) = P (A) + P (B) - P (A ∩ B)

Tres o mas eventos:

P (A U B U C) = P (A) + P (B) + P (C) - P (A ∩ B) - P (A ∩ C) - P (B ∩ C) + P (A ∩ B ∩ C)

Si son mutuamente excluyentes (independientes) :

P (A U B) = Ø

P (A U B) = P (A) + P (B)

Tres o mas eventos:

P (A U B U C) = P (A) + P (B) + P (C)

Probabilidad Condicional:

Muchas veces la probabilidad de que ocurra un suceso viene influida por el hecho de que ocurra o no otro suceso, o por una información adicional.

En general, si A y B son dos eventos , se define la probabilidad condicionada del eveto A sobre el B como la probabilidad de que ocurra A habiendo sucedido antes B:

$\begin{displaymath} \mathbb{P}(A \mid B) = \frac{\mathbb{P}(A \cap B)}{\mathbb{P}(B)} \end{displaymath}$

Regla de la multiplicacion:

Sean A y B dos eventos definidos en el espacio muestral S. Entonces :

P (A ∩ B) = P (B) . P (A/B)

o bien

P (A ∩ B) = P (A) . P (B/A)

Si A y B son eventos independientes entonces:

P (A ∩ B) = P (A) . P (B)

Probabilidad Total:

Sea A1, A2, ...,An un sistema completo de sucesos tales que la probabilidad de cada uno de ellos es distinta de cero, y sea B un suceso cualquier del que se conocen las probabilidades condicionales P(B/Ai), entonces la probabilidad del suceso B viene dada por la expresión:

Ejemplo:

P (F) = P (F ∩ A) + P (F ∩ A´)
= P (F/A) . P (A) + P (F/A´) . P (A´)

Teorema de Bayes:

Sea A1, A2, ...,An un sistema completo de sucesos, tales que la probabilidad de cada uno de ellos es distinta de cero, y sea B un suceso cualquier del que se conocen las probabilidades condicionales P(B/Ai). entonces la probabilidad P(Ai/B) viene dada por la expresión:

$\begin{displaymath} \mathbb{P}(A \mid B) = \frac{\mathbb{P}(B \mid A) \cdot \mathbb{P}(A)}{\mathbb{P}(B)} \end{displaymath}$

P (B) = P (B/A1) . P (A1) + P (B/A2) . P (A2)+...+ P (B/An) . P (An)

o bien:

El teorema de Bayes parte de una situación en la que es posible conocer las probabilidades de que ocurran una serie de sucesos Ai.

A esta se añade un suceso B cuya ocurrencia proporciona cierta información, porque las probabilidades de ocurrencia de B son distintas según el suceso Ai que haya ocurrido.

Conociendo que ha ocurrido el suceso B, la fórmula del teorema de Bayes nos indica como modifica esta información las probabilidades de los sucesos Ai.

En los problemas relacionados con la probabilidad, y en particular con la probabilidad condicionada, así como con la probabilidad total y el teorema de Bayes, es aconsejable que, con la información del problema, construyas una tabla de contingencia o un diagrama de árbol.

Probabilidad y Etadística Tec.